Hyper-Sparse Optimal Aggregation
Published in Journal of Machine Learning Research, 2011
S. Gaïffas and G. Lecué
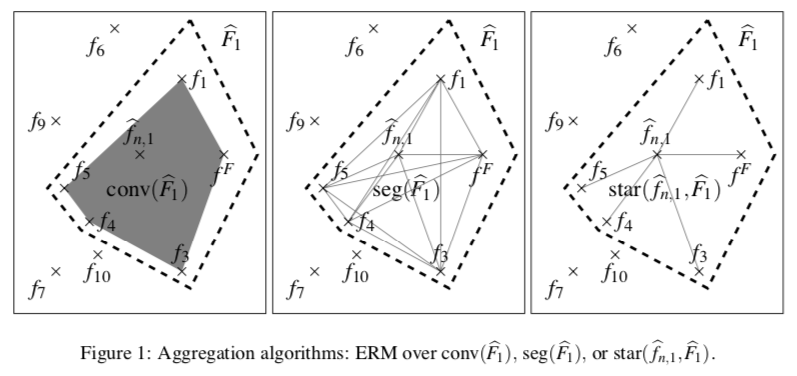
Given a finite set $F$ of functions and a learning sample, the aim of an aggregation procedure is to have a risk as close as possible to risk of the best function in $F$. Up to now, optimal aggregation procedures are convex combinations of every elements of $F$. In this paper, we prove that optimal aggregation procedures combining only two functions in $F$ exist. Such algorithms are of particular interest when $F$ contains many irrelevant functions that should not appear in the aggregation procedure. Since selectors are suboptimal aggregation procedures, this proves that two is the minimal number of elements of $F$ required for the construction of an optimal aggregation procedure in every situations. Then, we perform a numerical study for the problem of selection of the regularization parameters of the Lasso and the Elastic-net estimators. We compare on simulated examples our aggregation algorithms to aggregation with exponential weights, to Mallow’s $Cp$ and to cross-validation selection procedures.

