High-dimensional robust regression and outliers detection with SLOPE
Published in arXiv preprint, 2017
A. Virouleau, A. Guilloux, S. Gaïffas and M. Bogdan
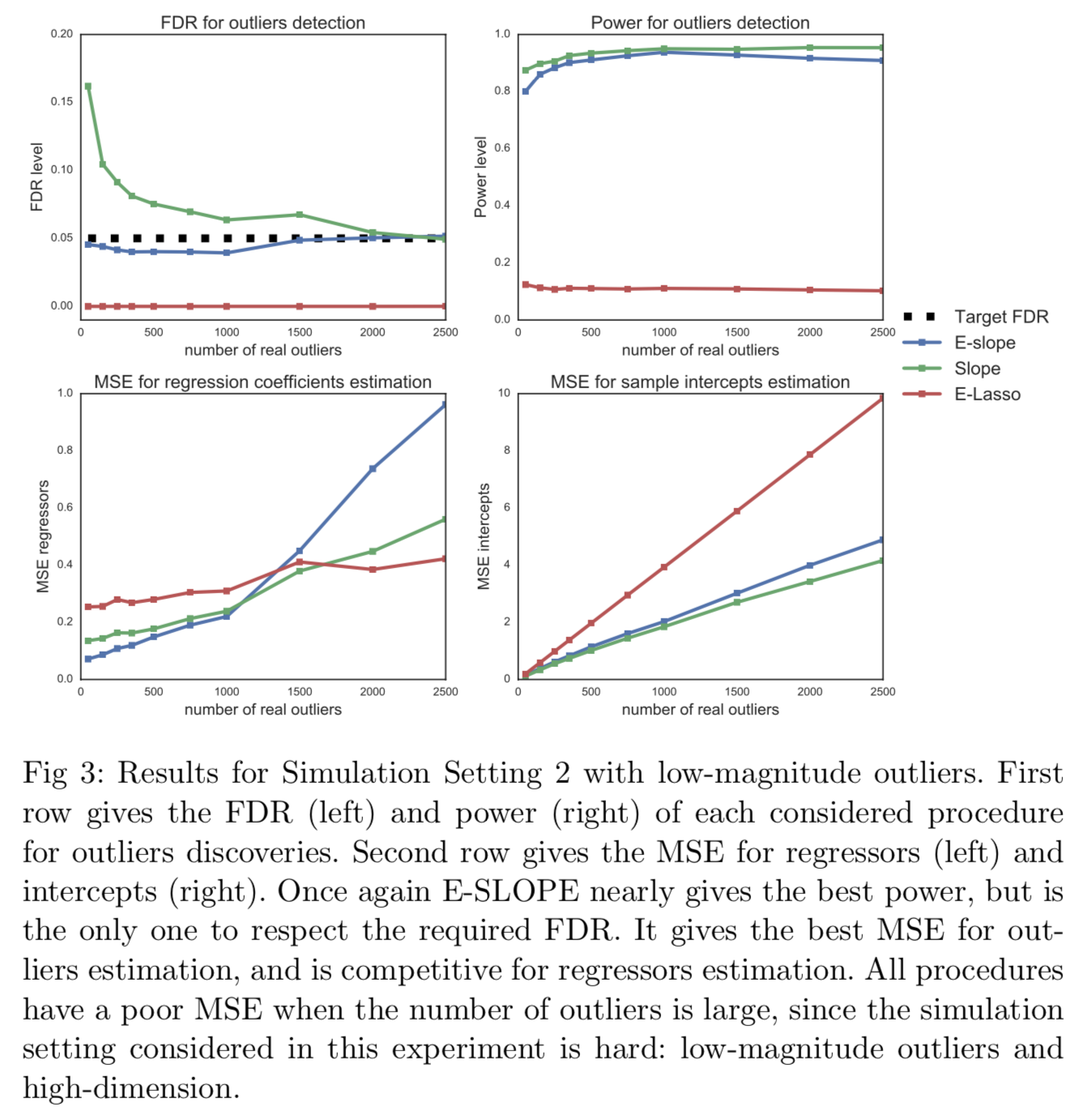
The problems of outliers detection and robust regression in a high-dimensional setting are fundamental in statistics, and have numerous applications. Following a recent set of works providing methods for simultaneous robust regression and outliers detection, we consider in this paper a model of linear regression with individual intercepts, in a high-dimensional setting. We introduce a new procedure for simultaneous estimation of the linear regression coefficients and intercepts, using two dedicated sorted-$\ell_1$ penalizations, also called SLOPE. We develop a complete theory for this problem: first, we provide sharp upper bounds on the statistical estimation error of both the vector of individual intercepts and regression coefficients. Second, we give an asymptotic control on the False Discovery Rate (FDR) and statistical power for support selection of the individual intercepts. As a consequence, this paper is the first to introduce a procedure with guaranteed FDR and statistical power control for outliers detection under the mean-shift model. Numerical illustrations, with a comparison to recent alternative approaches, are provided on both simulated and several real-world datasets. Experiments are conducted using an open-source software written in Python and C++.

