Sparse inference of the drift of a high-dimensional Ornstein–Uhlenbeck process
Published in Journal of Multivariate Analysis, 2018
S. Gaïffas and G. Matulewicz
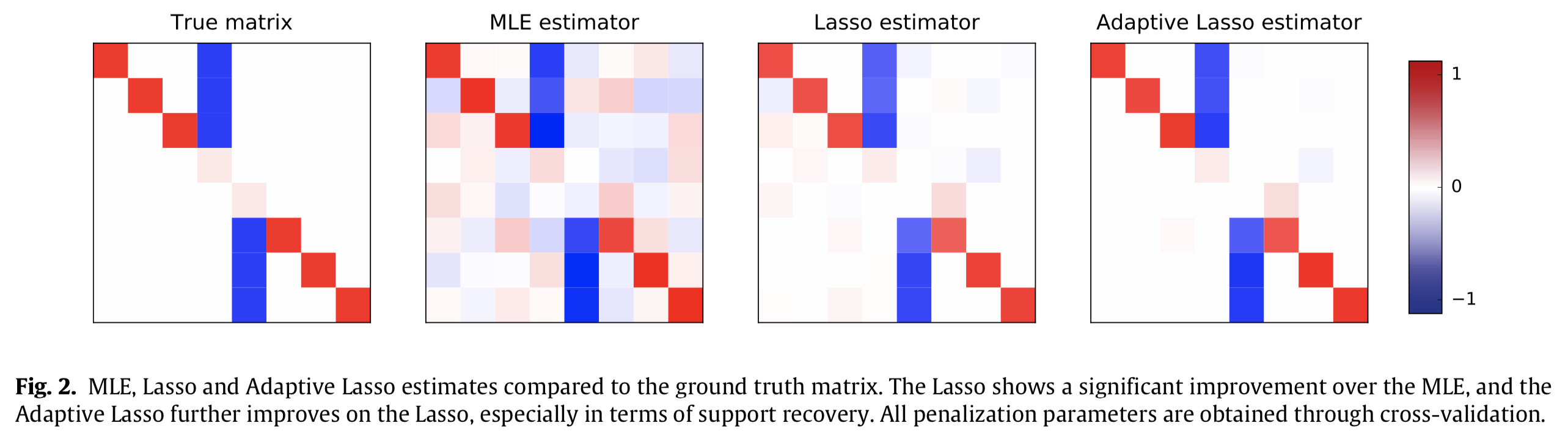
Given the observation of a high-dimensional Ornstein–Uhlenbeck (OU) process in continuous time, we are interested in inference on the drift parameter under a row-sparsity assumption. Towards that aim, we consider the negative log-likelihood of the process, penalized by an $\ell_1$-penalization (Lasso and Adaptive Lasso). We provide both finite and large-sample results for this procedure, by means of a sharp oracle inequality, and a limit theorem in the long-time asymptotics, including asymptotic consistency for variable selection. As a by-product, we point out the fact that for the Ornstein–Uhlenbeck process, one does not need an assumption of restricted eigenvalue type in order to derive fast rates for the Lasso, while it is well-known to be mandatory for linear regression for instance. Numerical results illustrate the benefits of this penalized procedure compared to standard maximum likelihood approaches both on simulations and real-world financial data.

