AMF: Aggregated Mondrian Forests for Online Learning
Published in Journal of the Royal Society Series B, 2021
J. Mourtada, S. Gaïffas and E. Scornet
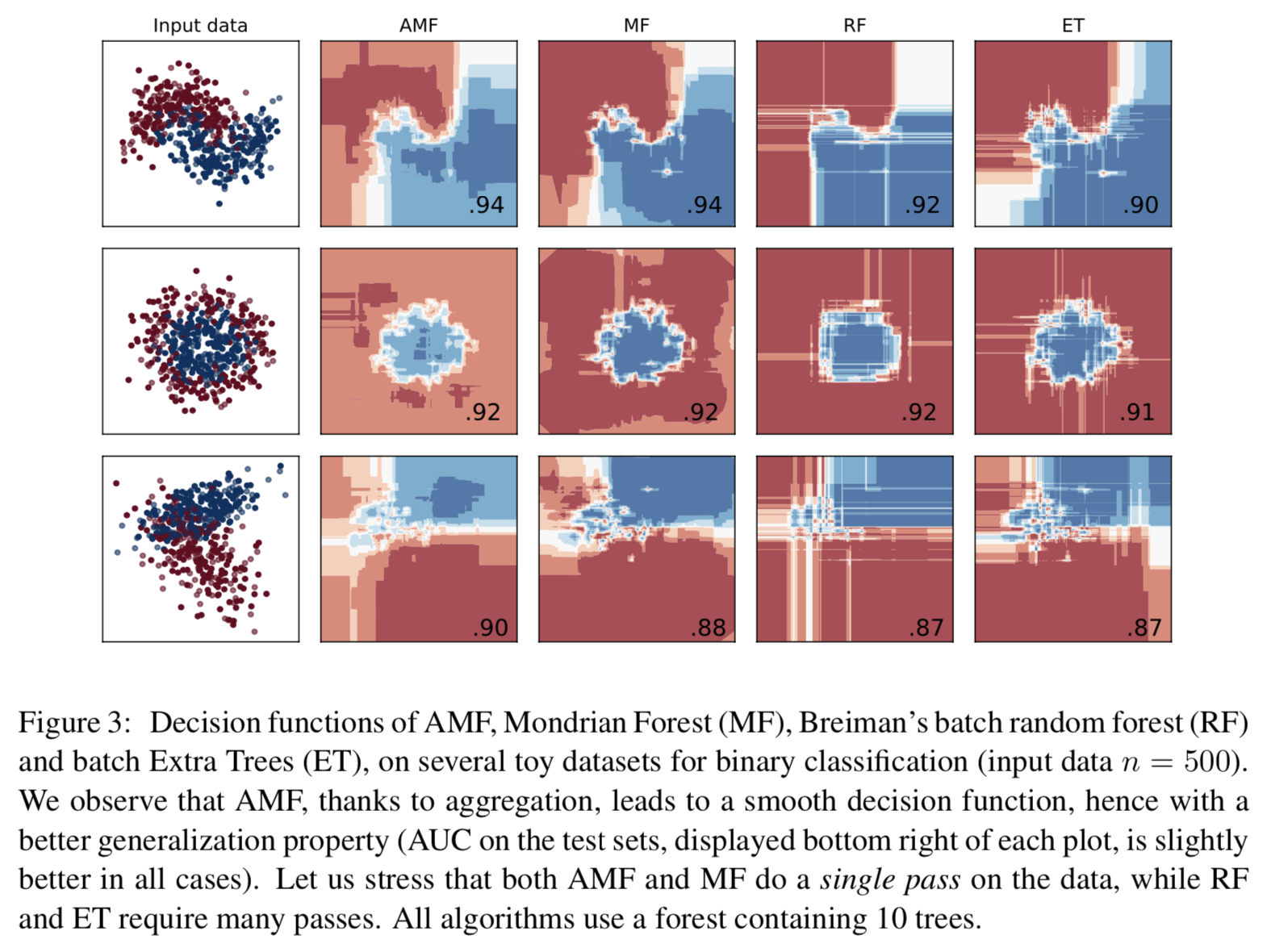
Random Forests (RF) is one of the algorithms of choice in many supervised learning applications, be it classification or regression. The appeal of such methods comes from a combination of several characteristics: a remarkable accuracy in a variety of tasks, a small number of parameters to tune, robustness with respect to features scaling, a reasonable computational cost for training and prediction, and their suitability in high-dimensional settings. The most commonly used RF variants however are ``offline’’ algorithms, which require the availability of the whole dataset at once. In this paper, we introduce AMF, an online random forest algorithm based on Mondrian Forests. Using a variant of the Context Tree Weighting algorithm, we show that it is possible to efficiently perform an exact aggregation over all prunings of the trees; in particular, this enables to obtain a truly online parameter-free algorithm which is competitive with the optimal pruning of the Mondrian tree, and thus adaptive to the unknown regularity of the regression function. Numerical experiments show that AMF is competitive with respect to several strong baselines on a large number of datasets for multi-class classification.

