Universal consistency and minimax rates for online Mondrian Forests
Published in NIPS, 2017
J. Mourtada, S. Gaïffas and E. Scornet
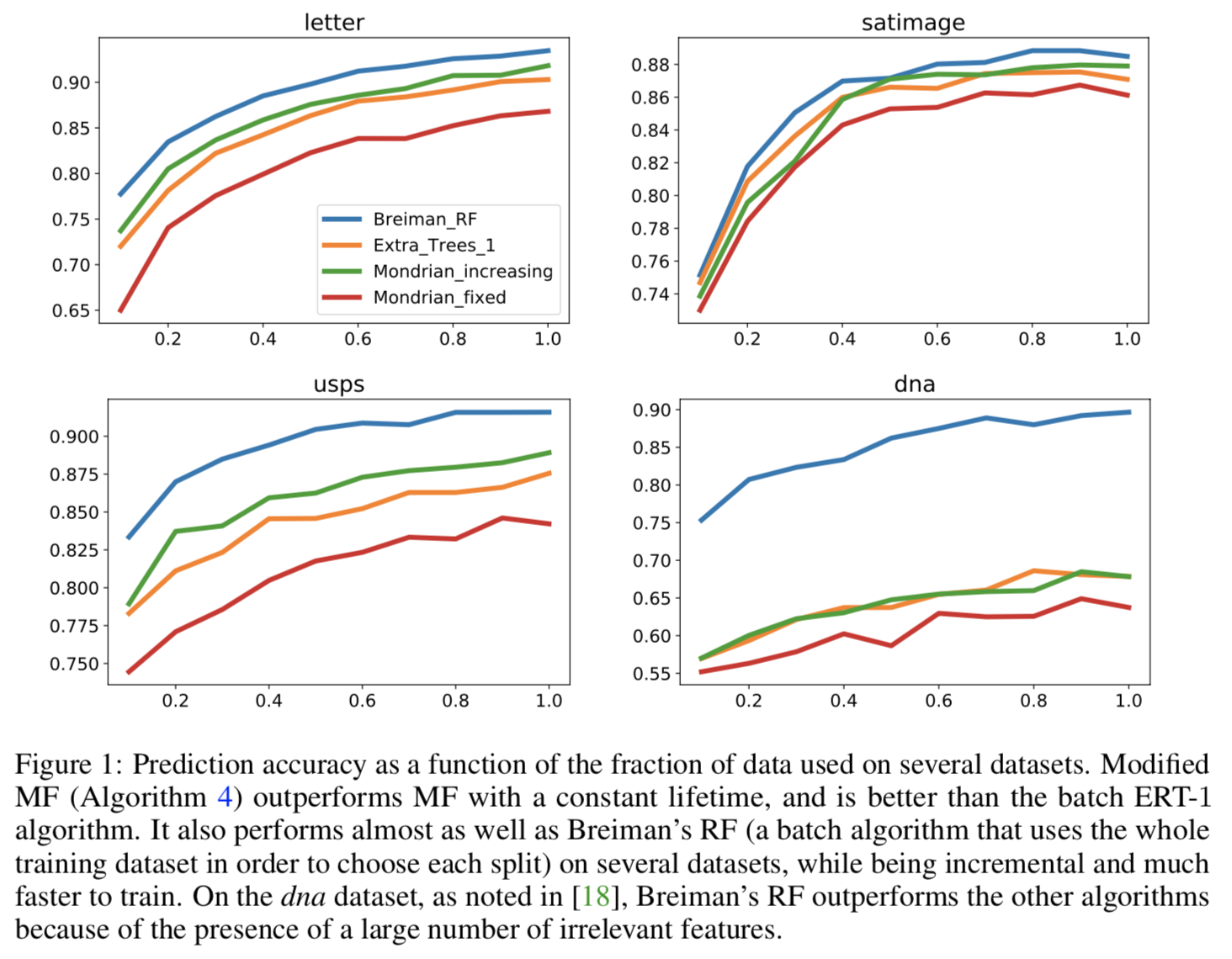
We establish the consistency of an algorithm of Mondrian Forests, a randomized classification algorithm that can be implemented online. First, we amend the original Mondrian Forest algorithm, that considers a fixed lifetime parameter. Indeed, the fact that this parameter is fixed hinders the statistical consistency of the original procedure. Our modified Mondrian Forest algorithm grows trees with increasing lifetime parameters $\lambda_n$, and uses an alternative updating rule, allowing to work also in an online fashion. Second, we provide a theoretical analysis establishing simple conditions for consistency. Our theoretical analysis also exhibits a surprising fact: our algorithm achieves the minimax rate (optimal rate) for the estimation of a Lipschitz regression function, which is a strong extension of previous results to an arbitrary dimension.

